The Lagrangian points (IPA: [lə.'grɒn.dʒi.ən] or [la.'grã.ʒi.ən]; also Lagrange point, L-point, or libration point), are the five positions in interplanetary space where a small object affected only by gravity can theoretically be stationary relative to two larger objects (such as a satellite with respect to the Earth and Moon). The Lagrange Points mark positions where the combined gravitational pull of the two large masses provides precisely the centripetal force required to rotate with them. They are analogous to geosynchronous orbits in that they allow an object to be in a "fixed" position in space rather than an orbit in which its relative position changes continuously.
A more precise but technical definition is that the Lagrangian points are the stationary solutions of the circular restricted three-body problem. For example, given two massive bodies in circular orbits around their common center of mass, there are five positions in space where a third body, of comparatively negligible mass, could be placed which would then maintain its position relative to the two massive bodies. As seen in a frame of reference which rotates with the same period as the two co-orbiting bodies, the gravitational fields of two massive bodies combined with the centrifugal force are in balance at the Lagrangian points, allowing the third body to be stationary with respect to the first two bodies.

History and concepts
In 1772, the famed Italian-French mathematician Joseph Louis Lagrange was working on the infamous three-body problem when he discovered an interesting quirk in the results. Originally, he had set out to discover a way to easily calculate the gravitational interaction between arbitrary numbers of bodies in a system, because Newtonian mechanics conclude that such a system results in the bodies orbiting chaotically until there is a collision, or a body is thrown out of the system so that equilibrium can be achieved. The logic behind this conclusion is that a system with one body is trivial, as it is merely static relative to itself; a system with two bodies is very simple to solve for, as the bodies orbit around their common center of gravity. However, once more than two bodies are introduced, the mathematical calculations become very complicated. A situation arises where you would have to calculate every gravitational interaction between every object at every point along its trajectory.
Lagrange, however, wanted to make this simpler. He did so with a simple conclusion: The trajectory of an object is determined by finding a path that minimizes the action over time. This is found by subtracting the potential energy from the kinetic energy. With this way of thinking, Lagrange re-formulated the classical Newtonian mechanics to give rise to Lagrangian mechanics. With his new system of calculations, Lagrange’s work led him to hypothesize how a third body of negligible mass would orbit around two larger bodies which were already orbiting one another, which at specific points in its orbit would become stationary relative to one of its host bodies (planets). These points were named “Lagrangian points” in Lagrange's honor.
In the more general case of elliptical orbits, there are no longer stationary points in the same sense: it becomes more of a Lagrangian “area”. The Lagrangian points constructed at each point in time as in the circular case form stationary elliptical orbits which are similar to the orbits of the massive bodies. This is due to Newton's second law (), where p = mv (p the momentum, m the mass, and v the velocity) is invariant if force and position are scaled by the same factor. A body at a Lagrangian point orbits with the same period as the two massive bodies in the circular case, implying that it has the same ratio of gravitational force to radial distance as they do. This fact is independent of the circularity of the orbits, and it implies that the elliptical orbits traced by the Lagrangian points are solutions of the equation of motion of the third body.

A diagram showing the five Lagrangian points in a two-body system (e.g. the Sun and the Earth)
The Lagrangian points
The five Lagrangian points are labeled and defined as follows:
L1
The L1 point lies on the line defined by the two large masses M1 and M2, and between them.
Example: An object which orbits the Sun more closely than the Earth would normally have a shorter orbital period than the Earth, but that ignores the effect of the Earth's own gravitational pull. If the object is directly between the Earth and the Sun, then the effect of the Earth's gravity is to weaken the force pulling the object towards the Sun, and therefore increase the orbital period of the object. The closer to Earth the object is, the greater this effect is. At the L1 point, the orbital period of the object becomes exactly equal to the Earth's orbital period.
The Sun–Earth L1 is ideal for making observations of the Sun. Objects here are never shadowed by the Earth or the Moon. The Solar and Heliospheric Observatory (SOHO) is stationed in a Halo orbit at the L1 and the Advanced Composition Explorer (ACE) is in a Lissajous orbit, also at the L1 point. The Earth–Moon L1 allows easy access to lunar and earth orbits with minimal delta-v, and would be ideal for a half-way manned space station intended to help transport cargo and personnel to the Moon and back.
L2
The L2 point lies on the line defined by the two large masses, beyond the smaller of the two.
Example: On the side of the Earth away from the Sun, the orbital period of an object would normally be greater than that of the Earth. The extra pull of the Earth's gravity decreases the orbital period of the object, and at the L2 point that orbital period becomes equal to the Earth's.
Sun–Earth L2 is a good spot for space-based observatories. Because an object around L2 will maintain the same orientation with respect to the Sun and Earth, shielding and calibration are much simpler. The Wilkinson Microwave Anisotropy Probe is already in orbit around the Sun–Earth L2. The future Herschel Space Observatory as well as the proposed James Webb Space Telescope will be placed at the Sun–Earth L2. Earth–Moon L2 would be a good location for a communications satellite covering the Moon's far side.
If M2 is much smaller than M1, then L1 and L2 are at approximately equal distances r from M2, equal to the radius of the Hill sphere, given by:
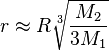
where R is the distance between the two bodies.
This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by .
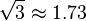
Examples:
Sun and Earth: 1,500,000 km from the Earth
Earth and Moon: 61,500 km from the Moon
L3
The L3 point lies on the line defined by the two large masses, beyond the larger of the two.
Example: L3 in the Sun–Earth system exists on the opposite side of the Sun, a little farther away from the Sun than the Earth is, where the combined pull of the Earth and Sun again causes the object to orbit with the same period as the Earth. The Sun–Earth L3 point was a popular place to put a "Counter-Earth" in pulp science fiction and comic books.
L4 and L5
The L4 and L5 points lie at the third point of an equilateral triangle whose base is the line between the two masses, such that the point is ahead of, or behind, the smaller mass in its orbit around the larger mass.
The reason these points are in balance is that at L4 and L5, the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycentre of the system. The barycentre being both the centre of mass and centre of rotation of the system, this resultant force is exactly that required to keep a body at the Lagrange point in orbital equilibrium with the rest of the system.
L4 and L5 are sometimes called triangular Lagrange points or Trojan points. The name Trojan points comes from the Trojan asteroids at the Sun-Jupiter L4 and L5 points, which themselves are named after characters from Homer's Iliad (the legendary siege of Troy).
Examples: The Sun–Earth L4 and L5 points lie 60° ahead of and 60° behind the Earth in its orbit around the Sun. They contain interplanetary dust. The Sun–Jupiter L4 and L5 points are occupied by the Trojan asteroids.
The giant impact hypothesis suggests that an object named Theia formed at L4 or L5 and crashed into the Earth after its orbit destabilized, forming the moon.
http://en.wikipedia.org/wiki/Lagrangian_point